
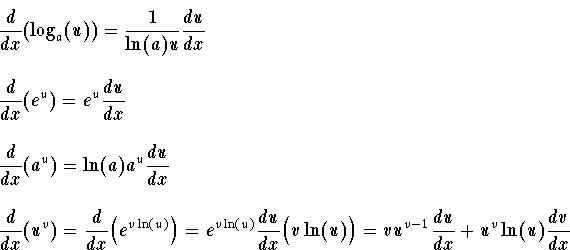
However, we can generalize it for any differentiable function with a logarithmic. Derivatives of Logs Replacing loge x with ln x back, we get d/dx (ln x) 1/x. In this case, unlike the exponential function case, we can actually find the derivative of the general logarithm function. Here, the interesting thing is that we have 'ln' in the derivative of 'log x'. We have denoted the input of $f$ (the tetrahedron) by the variable $x$. Derivatives of logarithmic functions are mainly based on the chain rule. (Videos) Derivatives of Logarithmic Functions Heres a video by patrickJMT where he goes through some examples of finding the derivative of a logarithmic. What is the Derivative of log x The derivative of log x (log x with base a) is 1/ (x ln a). However, it allows us to rewrite expectations in a way that is amenable to. To determine how to compute the derivative of the inverse of $f$, let's think about the derivative of $f$ in terms of the function machine metaphor. The log-derivative trick is really just a simple application of the chain rule. f ( x) is a function in terms of x and the natural logarithm of the function f ( x) is written as log e f ( x) or ln f ( x) in mathematics. Can we exploit this fact to determine the derivative of the natural logarithm? Here we present a version of the derivative of an inverse function page that is specialized to the natural logarithm. The derivative of logarithmic function can be derived in differential calculus from first principle. The natural logarithm $\ln(y)$ is the inverse of the exponential function. Or we could even write it as 1 over the natural log of b times the natural log of x. This is equal to the derivative with respect to x of the natural log of x over the natural log of b. So all we have to do is rewrite this thing. Differentiating and keeping in mind that lnb ln b is a constant, we see that. Log base e of x over log base e of b, which is the exact same thing as the natural log of x over the natural log of b. In this case, it is log (e), where e has a constant value (2.73) so it results into a constant.

If the base is other than e you need to multiply 1/x by the reciprocal of the natural logarithm of. As the logarithmic function with base, and exponential function with the same base form a pair of mutually inverse functions, the derivative of the logarithmic. Solving for y y, we have y lnx lnb y ln x ln b. Although the derivative of log (x) is 1/x where x is a variable. The derivative of a logarithmic function is given by: f (x) 1 / ( x ln (b) ) Here, x is called as the function argument. Other Lists of Derivatives: Simple Functions Trigonometric and Inverse Trigonometric Functions. The derivative of the exponential function $f(x)=e^x$ is the function itself: $f'(x)=e^x$. The derivative of the natural logarithmic function is 1/x. List of Derivatives of Log and Exponential Functions.

D d x ln x = 1 x \frac.\ _\square d x d lo g ( x 2 + 4 ) = x 2 + 4 2 x .


 0 kommentar(er)
0 kommentar(er)
